|
Canoe Body Yaw
by Lester Gilbert
On the pond, we know that a sailing boat is balanced by
either moving the sail plan forward to reduce weather helm or moving the sail
plan back to reduce lee helm. But why does the boat need “balancing” at all? Why
doesn’t she just sail straight ahead? And if she does need balancing, why does
the balance change with boat speed or heel angle?
Most texts discuss balance in terms of the yaw couple
generated by the difference between the offset center of effort of the sails
driving in one direction and the center of lift of the hull lifting in another,
as illustrated in figure 1. On my website
(Balance due to hull shape), I say that I’ve not found this
analysis at all useful. I’ll now be bolder and say that it is just wrong. The
reason is that the canoe body generates a very significant yaw moment by itself
when it is heeled, and this fact does not appear in this “explanation.”
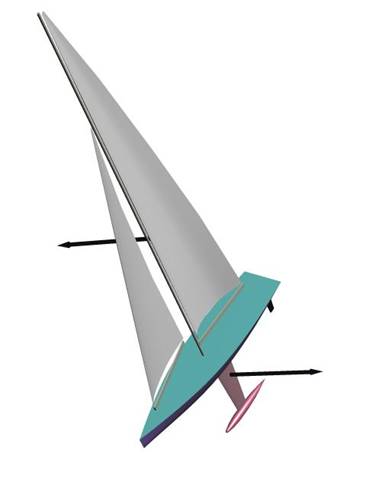
Figure 1. Illustration of
sail driving force and hull lifting force.
It is not widely known that a heeled canoe body naturally
luffs up. (To balance that, the sail plan must be moved forward, conceptually
holding the bow to leeward and counterbalancing the tendency of the hull to turn
to windward.) What is even less well known is what causes the canoe body to yaw
when heeled.
Waterplane
A favorite theory is since the heeled waterplane resembles an
airfoil section, the hull is developing lift. This is illustrated in figure 2
for a narrow transom hull and in figure 3 for a hull with a wide transom.
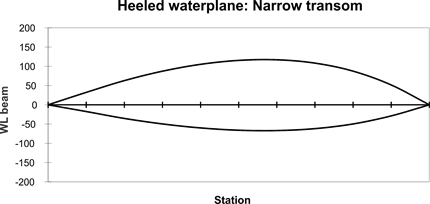
Figure 2. Waterplane shape
of heeled narrow transom hull.
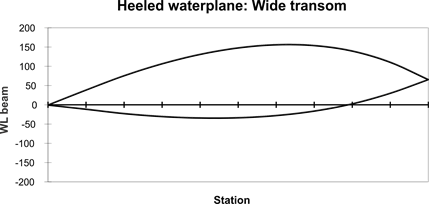
Figure 3. Waterplane shape
of heeled wide transom hull.
From this theory, it seems that a wide-transom design will
have a greater yaw moment, and if it is also a beamy design, an even greater yaw
moment. I’ve wanted to test this theory for some time, and have made a start
with Graham Bantock by running a heeled hull in the University of Southampton’s
Lamont towing tank. Graham brought his falling weight device (FWD) and two
hulls, Fraktal and Ikon, and I brought my Pikanto. (The FWD and the towing tank
arrangements were shown in an earlier article, in Issue 174,
Trim & Drag (AMYA MY #174).)
Hull designs
Ikon is one of the beamiest IOM designs (design LWL beam 187
mm, maximum beam 257 mm) with a relatively wide transom. Pikanto is a
“middle-of-the-road” design (design LWL beam 170 mm, maximum beam 210 mm), while
Fraktal is one of the narrowest IOMs (design LWL beam 163 mm, maximum beam 168
mm).

Figure 4. Lines of the
three designs tested.
Yaw moment
The yaw moment was estimated from the rudder angle needed to
keep the heeled canoe body tracking straight while being towed. Angles of
between 1 and 4.5 degrees were recorded.
Figure 5 plots rudder angle against heel for the three hull
designs, Fraktal, Ikon, and Pikanto. For each design, the graph plots rudder
angle when heeled at approximately 15 degrees at around 0.47 m/s, and when
heeled at approximately 25 degrees at around 1 m/sec.
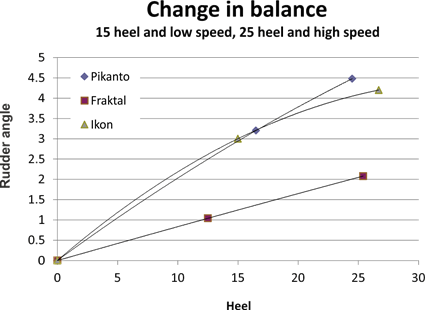
The yaw characteristics of Ikon and Pikanto are similar. Both
hulls yaw strongly when heeled. While the graph suggests that Ikon needs
slightly less rudder than Pikanto when heeled at around 25 degrees, this
difference is within measurement error. The yaw behaviour of Fraktal is rather
different. Overall, it yaws far less strongly. At around 15 degrees of heel,
Fraktal needs approximately 1.2 degrees of rudder to track true, while Pikanto
and Ikon require 3 or 3.2 degrees. In terms of practical boat balance on the
water, this is a very significant difference.
Figure 6 plots rudder angle against speed for the three hull
designs tested. For each design, as before, the graph plots rudder angle when
heeled approximately 15 degrees at around 0.47 m/s, and when heeled at
approximately 25 degrees at around 1 m/sec.
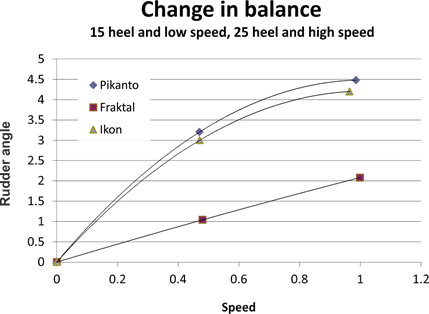
The general picture is similar to that of figure 5, in that
the yaw characteristics of Ikon and Pikanto are very similar, and of Fraktal,
rather different. The plot of yaw (rudder angle) against speed shows more
clearly that, for the heel angles and speeds tested, the yaw responses of Ikon
and Pikanto are characterized by a second degree polynomial, suggesting that
their yaw moment lessens with higher speed and heel. The yaw moment of Fraktal
against speed, however, is much lower and, for the heel angles and speeds
tested, linear. This suggests that Fraktal will show a steadily increasing yaw
moment as heel and speed increase. Hull speed for an IOM is approximately 1.3
m/s, and a visual extrapolation suggests that, for Ikon and Pikanto, yaw moment
(rudder angle) might reach a maximum of around 4.5 or 5 degrees, while for
Fraktal this maximum might be around 2.5 or 3 degrees. Such extrapolation is
merely suggestive, however; for while the hull might reach hull speed in a
reasonable wind, it will continue to heel as the wind builds, and an IOM can be
effectively raced at heel angles of up to 55 degrees.
Discussion and conclusions
In general, the results clearly and usefully demonstrate the
inherent tendency of a heeled canoe body to luff, proportionate to the degree of
heel.
In detail, the results are somewhat surprising. First is the
lack of difference in yaw moment between Ikon and Pikanto hull forms. Ikon is a
markedly beamy hull and when heeled generates a pronounced asymmetric waterplane.
Pikanto’s waterplane asymmetry is less pronounced and Pikanto was expected to
show significantly less yaw moment than Ikon.
Second, it was expected that Fraktal and Pikanto would be
much more similar in yaw moment, certainly at the lower heel angle, since
Fraktal’s significant vertical freeboard would not be expected to fully change
her sailing characteristics until well heeled. The hull lines of figure 4 show
that, generally speaking, the underwater hull forms of Pikanto and Fraktal are
more similar to each other than either is to Ikon.
Third, the unexpectedly linear response of Fraktal to changes
in heel and speed contrasts with the expected curvilinear responses of Ikon and
Pikanto.
The results do not support the “airfoil waterplane” theory of
canoe body yaw response to heel. This theory predicts Ikon should be different
from both Pikanto and Fraktal in terms of amount of yaw moment and how it
increases with heel; neither of these predictions was met.
As is usual in such experimental work, the data suggests the
need for further work to clarify the relationships observed among yaw moment,
canoe body design parameters, heel, and speed.
Acknowledgements
These experiments would not have been possible without Graham
Bantock’s enthusiasm and knowledge or without the support of Professor Philip
Wilson of the University of Southampton’s Department of Ship Science.
|
.htm_cmp_lghome010_bnr.gif)